DFS Trees

 You are given a connected undirected graph consisting of 

n$n$ vertices and m$m$ edges. The weight of the i$i$-th edge is i$i$.

Here is a wrong algorithm of finding a minimum spanning tree (MST) of a graph:

vis := an array of length n
s := a set of edges

function dfs(u):
    vis[u] := true
    iterate through each edge (u, v) in the order from smallest to largest edge weight
        if vis[v] = false
            add edge (u, v) into the set (s)
            dfs(v)

function findMST(u):
    reset all elements of (vis) to false
    reset the edge set (s) to empty
    dfs(u)
    return the edge set (s)

Each of the calls findMST(1), findMST(2), ..., findMST(n) gives you a spanning tree of the graph. Determine which of these trees are minimum spanning trees.

Input

The first line of the input contains two integers n$n$, m$m$ (2≤n≤105$2\le n\le {10}^5$, n−1≤m≤2⋅105$n-1\le m\le 2\cdot {10}^5$) — the number of vertices and the number of edges in the graph.

Each of the following m$m$ lines contains two integers ui$u_i$ and vi$v_i$ (1≤ui,vi≤n$1\le u_i,v_i\le n$, ui≠vi$u_i\ne v_i$), describing an undirected edge (ui,vi)$(u_i,v_i)$ in the graph. The i$i$-th edge in the input has weight i$i$.

It is guaranteed that the graph is connected and there is at most one edge between any pair of vertices.

Output

You need to output a binary string s$s$, where si=1$s_i=1$ if findMST(i) creates an MST, and si=0$s_i=0$ otherwise.

Examples

input

Copy

5 5
1 2
3 5
1 3
3 2
4 2

output

Copy

01111

input

Copy

10 11
1 2
2 5
3 4
4 2
8 1
4 5
10 5
9 5
8 2
5 7
4 6

output

Copy

0011111011

Note

Here is the graph given in the first example.

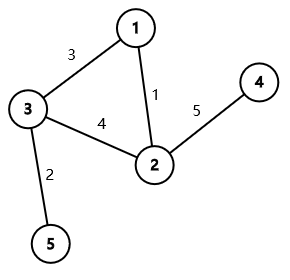
There is only one minimum spanning tree in this graph. A minimum spanning tree is (1,2),(3,5),(1,3),(2,4)$(1,2),(3,5),(1,3),(2,4)$ which has weight 1+2+3+5=11$1+2+3+5=11$.

Here is a part of the process of calling findMST(1):

• reset the array vis and the edge set s;
• calling dfs(1);
• vis[1] := true;
• iterate through each edge (1,2),(1,3)$(1,2),(1,3)$;
• add edge (1,2)$(1,2)$ into the edge set s, calling dfs(2):
  • vis[2] := true
  • iterate through each edge (2,1),(2,3),(2,4)$(2,1),(2,3),(2,4)$;
  • because vis[1] = true, ignore the edge (2,1)$(2,1)$;
  • add edge (2,3)$(2,3)$ into the edge set s, calling dfs(3):
    • ...

In the end, it will select edges (1,2),(2,3),(3,5),(2,4)$(1,2),(2,3),(3,5),(2,4)$ with total weight 1+4+2+5=12>11$1+4+2+5=12>11$, so findMST(1) does not find a minimum spanning tree.

It can be shown that the other trees are all MSTs, so the answer is 01111.